金属材料の機械的強度や特性はミクロの組織的構造に基づくため、より高性能な材料を得るためにはミクロなダイナミクスの解明が必要です。近年、材料の相転移や相分離などの解明に非平衡統計力学から導出されるフェーズフィールド・モデルが注目されています。導出される方程式は時間空間の偏微分方程式であり、空間の離散化によりメモリへのステンシル計算となります。フェーズフィールド・モデルは複雑な非線形項を多く含むため1格子点あたりの演算量が多く、CPUでは殆どの場合が2次元計算までしか行われてきませんでした。
フェーズフィールド・モデルは非平衡統計物理学から導出され、分子スケールとマクロなスケールの中間のメソスケールの現象を記述できます。秩序変数 φ (フェーズフィールド変数)を導入し、固相部分にφ=1を、液相部分にφ=0を設定します。界面を含む領域ではφが0から1へと急峻かつ滑らかに変化する拡散界面として扱われ、φ=0.5が界面として扱われます。
二元合金のデンドライト凝固成長ではフェーズフィールド・モデルから導出される界面エネルギーの異方性を考慮したAllen-Cahn方程式と溶質濃度についての時間発展方程式を解きます。CUDAを用い3次元直交格子上で2次精度有限差分法で離散化し1次精度の陽的時間積分(オイラー法)を行います。フェーズフィールド変数、濃度変数は全てGPUのビデオメモリ(CUDAではグローバルメモリと呼ばれる)上に確保し、計算途中ではPCI-Express Bus を介したGPUからCPUへのデータ通信を可能な限り行わないようにしました。格子点 (i, j, k)上のフェーズフィールド変数φと濃度変数cを時間積分するために必要な隣接格子点へのステンシル・アクセスを図1に示します。フェーズフィールド変数φは19格子点、濃度変数cは7格子点をメモリから読み込み、2回書き出します。
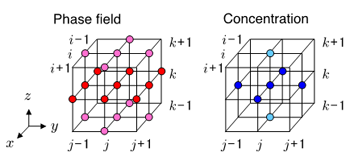
図1 フェーズフィールド・モデルによる凝固計算のステンシル
大規模な凝固計算を行うために、複数のGPUを用いてGPU単位での並列化を行います。メモリアクセスパターンを効率化するため、敢えて3次元分割ではなく、y方向、z方向に分割する2次元の領域分割法を用います。各GPUが分割された領域の計算を担当し、複数CPU計算と同じように隣接するGPU間での境界領域のデータ交換が必要になります。しかしGPUはノードを超えて他のGPUのグローバルメモリ上のデータに直接アクセスすることができないため、GPU間のデータ転送はホストCPUのメモリを経由し、次の3段階で構成されます。(1) CUDAランタイムライブラリによるGPUからCPUへの転送、(2) MPIライブラリによるCPU間のデータ転送、(3) CUDAランタイムライブラリによるCPUからGPUへの転送。 |
|
各GPUが担当する計算領域を、y方向の境界領域、z方向の境界領域、それらを除いた中心領域に分割し、y、z方向の境界領域をCPUで計算し中心領域をGPUで計算させます。先行研究では境界も中心領域もGPUで計算したが、ここでは境界領域をCPUで計算しGPU計算の関数を分割することなく通信の隠蔽を実現しました。ただしこの手法は、全計算領域サイズによってCPUによる通信と境界領域の計算にかかる時間が中心領域のGPU計算時間よりも長いことがあり、CPUがしばしばボトルネックとなります。凝固計算では、z方向の境界領域はGPUで計算する方が実行性能が良いことが分かりました。TSUBAME 2.0の各ノードには3個のGPU と12個のCPU cores が搭載されているので、境界領域の計算に4個のCPU cores を割り当て、Open MPを用いて並列計算しています。
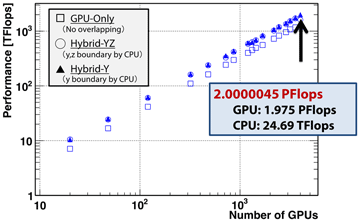
図2 フェーズフィールド・モデルによる凝固計算のTSUBAME 2.0 における弱スケーリング
TSUBAME 2.0 の多数の GPU(M2050)を用い、Al-Si合金の凝固成長に対する大規模計算を行いました。1個のGPUが担当する計算領域のサイズを一定にし、GPU数を増やしたときの弱スケーリング性能を測定しました。ビデオメモリのサイズから、1個のGPUの計算格子サイズは単精度計算では4096×128×128としています。4000GPUを利用して4096×6500×10400格子での計算では、単精度で2.0000045 PFlops という極めて高い実行性能を達成しました。実用的な格子計算のアプリケーションとしては、世界で初めてペタスケールを超えたと言えます。
参考文献
| [1] |
R. Kobayashi: Modeling and numerical simulations of dendritic crystal growth. Physica D, Nonlinear Phenomena, 63(3-4), 410 - 423 (1993) |
| [2] |
小川慧, 青木尊之, 山中晃徳: マルチGPUによるフェーズフィールド相転移計算のスケーラビリティー ― 40GPUで5 TFLOPSの実効性能, 情報処理学会論文誌コンピューティングシステムVol. 3 No. 2 67-75 (2010 June) |
| [3] |
A. Yamanaka, T. Aoki, S. Ogawa, and T. Takaki: GPU-accelerated phase-field simulation of dendritic solidification in a binary alloy. Journal of Crystal Growth, 318(1):40 - 45 (2011). The 16th International Conference on Crystal Growth (ICCG16)/The 14th International Conference on Vapor Growth and Epitaxy (ICVGE14) |
| [4] |
T. Shimokawabe, T. Aoki, T. Takaki, A. Yamanaka, A. Nukada, T. Endo, N., Maruyama, S. Matsuoka: Peta-scale Phase-Field Simulation for Dendritic Solidification on the TSUBAME 2.0 Supercomputer, in Proceedings of the 2010 ACM/IEEE International
Conference for High Performance Computing, Networking, Storage and Analysis, SC’11, IEEE Computer Society, Seattle, WA, USA, Nov. 2011, SC’11 Technical Papers, 2011/11. |
|