Research
IDO Scheme(Non-conservative Form)
局所補間微分オペレータ
さまざまな分野で重要となる現象の殆どは偏微分方程式で記述されます。一般に偏微分方程式の数学的な解析解を求めることはまず不可能ですから、数値計算で精度の高い近似解を求めることが大変重要となります。つまり、すばらしい偏微分方程式の数値計算手法を開発すれば、さまざまな分野で非常に役に立つということです。これまで分からなかったことを解明したり、未来を予測したりできるのです。 コンピュータを使って時間・空間に関する偏微分方程式を解くためには、解こうとする時間・空間の範囲を離散(格子)化する必要があります。これまでは、微分を差分で置き換える有限差分法や有限体積法、有限要素法などが使われてきました。我々は新しい数値計算手法として、局所補間微分オペレータ(IDO: Interpolated Differential Operator) 法を開発しています。今まで解くことのできない問題に適用することが目的であり、高精度かつ安定性とコンパクト性を有した数値計算スキームです。ただ、差分法などに比べると、多少の計算量と必要なメモリーが増えますが、コンピュータの能力は急速に進歩していますから問題ではありません。IDO法は3つの重要な要素 (1)局所補間、(2) 微分演算、(3) 逐次オペレータ法から構成されています。 |
|
|
青木研究室で行われている数値シミュレーションの殆どはIDO法に基づいてコードが組まれています。数値計算精度や多次元拡張性の検証、非線型方程式への適用、圧縮性および非圧縮性流体問題への適用(レーリーテーラー不安定性、乱流の直接計算、風音解析、電磁場計算等)、複雑な界面の取り扱い(樹枝状結晶成長、舞い落ちる枯葉のシミュレーション、血流計算)等、基礎的研究から応用研究に至るさまざまな研究に使われています。 |
||
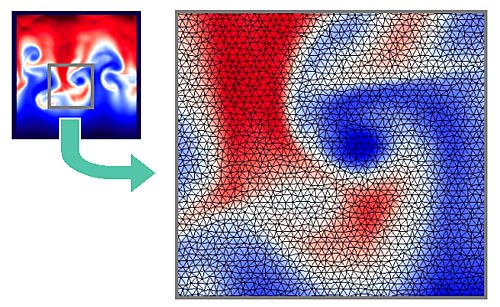
レーリーテーラー不安定性の成長過程を非構造(3角形)格子で計算した例。
- 参考文献
- T. Aoki: Interpolated Differential Operator (IDO) Scheme for Solving Partial Differential Equations, Comput. Phys. Comm. Vol.102, No.1-3 (1997) 132-146.
- K. Sakurai, T. Aoki: Implicit IDO (Interpolated Differential Operator) Scheme, Comput. Fluid Dynamics Journal, Vol.8, No. 1 (1999) 6-12.
- T. Aoki, S. Nishita, K. Sakurai: Interpolated Differential Operator (IDO) Scheme and Application to Level Set Method, Comput. Fluid Dynamics Journal , Vol.9, No.4 (2001) 406-417
- K. Sakurai, T. Aoki: A Numerical Procedure to Evolving Contact Discontinuity by using Moving Cut-Cell Method, Comput. Fluid Dynamics Journal, Vol.10, No.1 (2001), 76-84
- 青木尊之, 肖 鋒: 複雑形状の複雑でない計算法, 情報処理, Vol. 42, No.6 (2001), 550-556
- T. Aoki: 3D simulation for falling papers, Comput. Phys. Comm., Vol.142 (2001) 326-329
- K. Sakurai, T. Aoki, W. H. Lee, and K. Kato: Poisson Equation Solver with Fourth-Order Accuracy by using Interpolated Differential Operator Scheme, Comput. Math. Appl. Vol.43, (2002) 621-630
解説:局所補間
離散化されたi番目の格子点上で物理量fに関する方程式を解く場合に説明します。周囲の格子点のfの値をできるだけ数多く用いて補間関数を構成すれば高い精度が得られますが、補間関数の局所性(コンパクト性)が失われます。そこで、全ての格子点で物理量fに加えてその空間微係数fxも解くことにします。fとfxを独立に与えて値と勾配まで滑らかにつながるエルミート補間を用いることにより、高精度かつコンパクトな補間関数を得ることができます。
我々は2種類の補間範囲を使います。1つは風に流されて物が移動してくるように情報も風上から運ばれてくるという考え方に基づいた風上補間です。移動する速度が正の場合u(i) > 0 には、補間関数F(x) を格子点 i - 1 〜 i の範囲に形成します。負の場合には格子点 i 〜 i + 1 の範囲に形成します。2つの格子点にそれぞれ物理量とその空間微係数で合わせて4つの条件がありますから、多項式を使うならば3次になります。
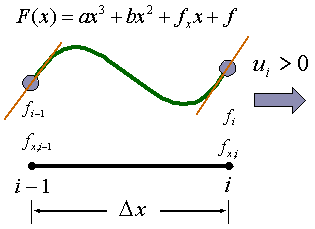
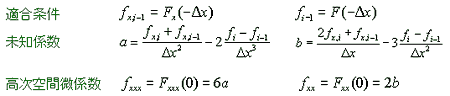
この補間関数は流体方程式の移流項などに適用します。
もう一つの補間関数は、格子点iを中心に i - 1 〜 i + 1 の範囲をカバーする中心補間です。音波や熱伝導は全ての方向に伝播しますから、このような範囲の補間関数が必要です。3つの格子点上に物理量とその空間微係数の情報がありますから、5次の多項式を構成することができます。
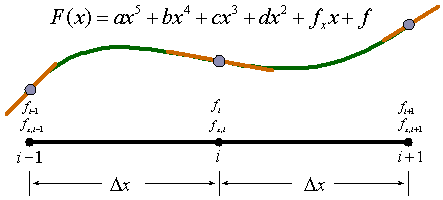
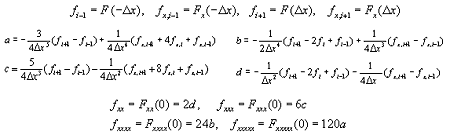
中心補間はポアソン方程式、流体方程式の粘性項などの2階以上の空間微分項に使われます。空間精度としては4次精度を持っています。
解説:微分演算
IDO法は偏微分方程式中に現れる微分項に対して差分式などで置き換えるのではなく、補間関数を偏微分方程式の近似解と見なすので、微分項は補間関数に対する微分演算として扱います。
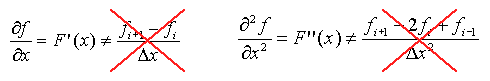
ただし、補間関数を多項式で形成しているので、微分できる最高の階数は風上補間の場合には3階、中心補間の場合には5階となります。さらに高階微分が必要な場合にはコンパクト性を犠牲にして周囲の4点から補間関数を生成したり、2階微分までを独立に与える方法もありますが、殆どの問題は上で説明した補間関数で十分です。
解説:逐次オペレータ
IDO法では偏微分方程式自体も微分オペレータと見なすので、テーラー展開をもとに高次の時間精度まで時間積分を行うことができます。解きたい方程式が次のような形だと仮定します。
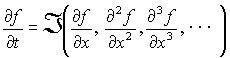
時間に関するテーラー展開を行うと、
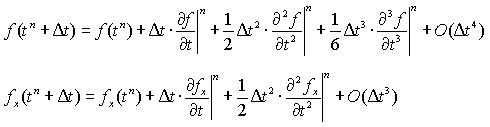
のように時間の高階微係数が必要になります。そこで、基礎方程式を繰り返しオペレートすることで、次のように時間の高階微分項を空間の高階微分項に置き換えることができます。
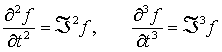
高階の空間微分項は補間関数を微分することにより簡単に求められます。
解説:Burgers方程式の解法例
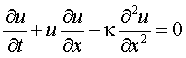
1次元のBurgers 方程式をIDO法で解くプロセスを示します。uとuxの時間積分をするために、テーラー展開に現れる時間微分項を以下のように空間微分に置き換えます。κは正の粘性定数です。
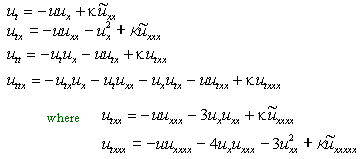
2階以上の微分項に対して、チルダの付いた項は粘性項から導かれているので中心補間を用います。それ以外の高階微分項は移流項からきているので風上補間を用います。
初期条件として、100 < x では u = 1.0, x > 100 では u = − 0.5 のステップ状の衝撃波プロファイルを仮定します。Burgers方程式の弱解は、衝撃波面は速度 us = (1.0 - 0.5)/2 = 0.25 で右側に移動することになっています。
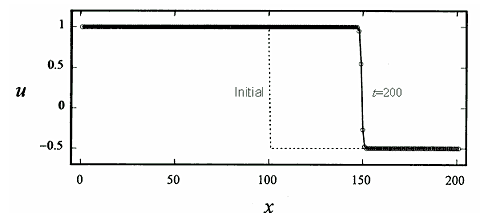
数値計算結果では、t = 200 で衝撃波面は x = 150 の位置にあり、理論どおりになっていることが分かります。少し専門的になりますが、通常のIDO法は非保存形で離散化式を解いているので、κがゼロでは保存されずないために小さな値を持つことが必要です。